Frequency converter
How to avoid typical pitfalls when measuring Variable Frequency Drives
by Dipl.-Ing. Thomas Jäckle, ZES ZIMMER R&D
Increased political and public focus on optimizing resource utilization has been one of the drivers behind the increased adoption of Variable Frequency Drives (VFDs) for motor control. Manufacturers of motors and drive systems are under pressure to improve the efficiency of their products, which requires suitable test and measurements equipment to quantify both consumption and losses in turn. While VFDs have the potential to improve overall efficiency, they also increase complexity and thus demand a higher level of sophistication in measurement.
With regard to adequate measuring methodology and assessment of results, these are some of the typical questions:
How can the level of accuracy be estimated reliably? Can PWM pulses of short duration also be measured correctly? How do instrument settings impact the final result? Is the available sampling rate sufficient for the purpose?
The following application note not only answers the above questions, it also provides some useful background information on electrical power analysis in general.
Measurement uncertainty in relation to spectral distribution of power
Targeting efficiency improvements in the tenth-of-a-percent range inevitably requires close scrutiny of the employed measurement procedures. Every subsequent observation regarding power also applies to efficiency, which is defined as the ratio of output to input power of a given device. Power analyzer manufacturers usually only define accuracies for sinusoidal signals, since the national standards to which their instruments are traced back to only encompass such. Despite this limitation, there are still ways to reliably estimate uncertainty for typical real-world signals.
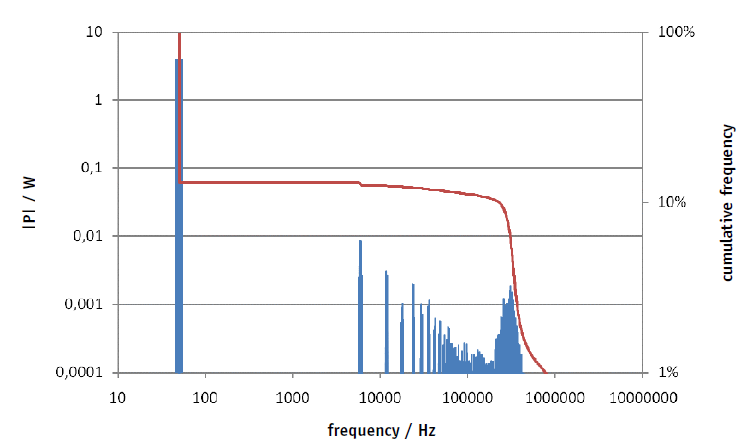
The power spectrum at a VFD’s output exhibits the following characteristics. While the exact numerical values are a function of the concrete application, the governing principle is always identical.
The dominant contribution to RMS power stems from the motor’s fundamental frequency. Assuming reasonable efficiency of the motor-drive combination, a large part of overall energy will be conveyed from the VFD to the motor at this frequency. It is typically situated below 1000 Hz and shows low harmonic content.
The next contributor is the VFDs switching frequency, which is situated somewhere between a few hundred Hertz (VFDs with power level of multiple MW) and 20 kHz (kW power level) and is polluted with a high harmonic content due to the quasi-rectangular signals of the pulse width modulation (PWM).
Lastly, some signal content of various origins is to be found as high up as the MHz range: e.g. resonances in the motor windings caused by rectangular waves, steep signal flanks, end-of-line reflections, et cetera.
By principle active power can only be transferred by voltages and currents of the same frequency. Evidently, if the motor rotates, active power is present. At and above the PWM switching frequency the current is highly dependent on inductance and the capacitance of the windings and the earth capacitance of the motor. Such currents may be attenuated and phased shifted - either by inductance or capacitance. It is important to note that even under worst case conditions their contribution to active power is only a tiny fraction of the fundamental’s. Regarding the upper end of the measurable spectrum, any observable currents will only be of very limited magnitude, which, combined with relatively low voltages will only yield negligible amounts of power, if at all.
In our example, a small motor is running idle at 50Hz (4W). The VFD has a switching frequency of 6 kHz and drives the motor via a 100 meter cable. These non-typical settings have been chosen to more better illustrate a number of phenomena shown in Figure 1: The signal components of the switching frequency (6 kHz, 18 kHz, 30 kHz,…) - highlighted in blue in the diagram – stand out more clearly as they would for a motor with load. Nevertheless, the amplitude steadily declines in the range from 6 kHz to 150 kHz. The subsequent re-increase peaking at 310 kHz is caused by reflections due to the purposefully exaggerated length of the cable.
The red curve shows the (inverted) cumulative distribution function of active power. The major part (87%) is caused by the fundamental at 50 Hz, the remaining 13% are higher in frequency. Starting at the switching frequency of the converter (6 kHz), remaining power tapers off. The example shows one last peak at 310 kHz after which the remaining power drops from 11% to 1%.
Although the amplitude at 310 kHz is lower than it is at 6 kHz, the reflections are distributed over a broader part of the spectrum and thus surpass the direct contribution of the switching frequency, which is illustrated by size of the blue area.
A cable length of 100 meters is rather unusual, as are the reflections caused by this, and we like to point out that the basic principle of this measurement is true even under more realistic circumstances. In order to correctly assess the level of accuracy, the present spectral components within the system need to be determined and measured.
As mentioned above, the parameters used are not typical for real-world scenarios. Since the reflections mainly are a function of cable length, 100m leads will rather be the exception than the rule. What is important to keep in mind is the underlying principle: before attempting to estimate uncertainties, the spectral distribution of power needs to be known.
Spectral analysis of the VFD’s output allows estimation of the accuracy contribution of each frequency range. Due to its sinusoidal nature, the fundamental, main contributor to active power, is easiest to assess. Although for higher-frequency components we have to resort to approximation, the errors introduced are negligible, as the following examples will show.
Example 1
Assume the following spectral distribution of power:
₋ 4 W @ 5 Hz fundamental
₋ 0.1 W caused by switching frequency and harmonics in the range of 6 kHz to 150 kHz
₋ 0.03 W caused by RF effects @ 350 kHz
8W will be assumed for the power measuring range. The measuring accuracy in the table below was taken from the LMG500’s specifications. More information about calculating the total uncertainty of a non-sinusoidal signal can be found in the user manual accompanying each ZES ZIMMER power analyzer.
| Frequency range |
0.05 Hz...45 Hz, 65 Hz...3 kHz |
45 Hz...65 Hz | 15 kHz...100 kHz | 100 kHz...500 kHz |
|
Accuracy of active power ±(% of reading + % of range) |
0.028+0.03 | 0.015+0.01 | 0.24+0.3 | 0.8+1.0 |
The fundamental shows an uncertainty of 0.028% of 4 W = 1.12 mW. Although the VFD’s pulse-width modulation operates at 6 kHz, we have chosen the range from 15 kHz to 100 kHz in Table 1 for switching frequency and harmonics. The slight over-estimation caused thereby is compensated by the under-estimation of the error for frequencies above 100 kHz, which helps to simplify the following calculation significantly. Hence, the switching frequency contributes an uncertainty of 0.24% of 0.1 W = 0.24 mW and the RF effects contribute an uncertainty of 0.8% of 0.03 W = 0.24 mW.
In addition to the uncertainty of the measured signals we have to consider the uncertainty contributed by the measuring range as well. Choice of range is determined by the signal with the highest amplitude, i.e. 5Hz. Thus we arrive at 0.03% of 8W = 2.4mW, and total uncertainty can be calculated as 1.12 mW + 0.24 mW + 0.24 mW + 2.4mW = 4mW:
| Measuring error from measuring range: | 2.40 mW/4 mW = | 60% |
| Measuring error from fundamental: | 1.12 mW/4 mW = | 28% |
| Measuring error from switching frequency: | 0.24 mW/4 mW = | 6% |
| Measuring error from RF effects: | 0.24 mW/4 mW = | 6% |
Example 2
Same as Example 1, but 50 Hz fundamental.
Now the fundamental contributes an uncertainty of 0.015% of 4W = 0.6mW. The error caused by the measuring range decreases to 0.01% of 8 W = 0.8 mW. Thus the total uncertainty becomes 1.88 mW.
Again, the signal uncertainty contributions are
| Measuring error from measuring range: | 0.80 mW/1.88 mW = | 42% |
| Measuring error from fundamental: | 0.60 mW/1.88 mW = | 32% |
| Measuring error from switching frequency: | 0.24 mW/1.88 mW = | 13% |
| Measuring error from RF effects: | 0.24 mW/1.88 mW = | 13% |
Although the higher frequencies now exert a stronger impact on the total, the measuring error stemming from the fundamental at 50 Hz is still dominating. Whether the measuring error from the switching frequency is estimated as 0.24 mW or 0.3 mW represents a relative difference of 25%, but only results in a 3% difference with regard to total error.
It still needs to be clarified how to determine the exact spectral distribution, considering that not all signal components are harmonics. One approach is the use of filters: Start with a low pass filter with a cut-off frequency below the switching frequency (e.g. 1 kHz) to isolate the fundamental and its harmonics. Repeat with a cut-off frequency above the switching frequency but below the RF (e.g. 150 kHz) part. The difference between both values equals the power contribution of the switching frequency.
Figure 1 was generated in a different manner: ZES ZIMMER’s Waveform Analysis tool (available as option for the LMG500 precision power analyzer) offers analysis of the frequency spectrum with configurable resolution. For the above example we chose 50Hz, resulting in a very detailed power spectrum consisting of 30,000 individual lines between 50Hz and 1.5MHz.
Importance of cycle / measurement time
There are two possible reasons preventing the correct measurement of an integer number of signal cycles: On the one hand, synchronization may be misconfigured, resulting in synchronization to the wrong frequency, or none at all. On the other hand, the signal period may actually be longer than the duration of the measurement, in which case only a fraction of the cycle will be captured. For example, a 0.55 Hz signal cannot be measured correctly within 1 second. The latter case can easily be avoided by adjusting the instrument’s cycle time.
In case the measurement time cannot be set accurately, the measuring error can be reduced by choosing a longer interval. Being off by 0.1 periods results in a relatively larger error when measured over 1.1 periods than when measuring over 100.1 periods!
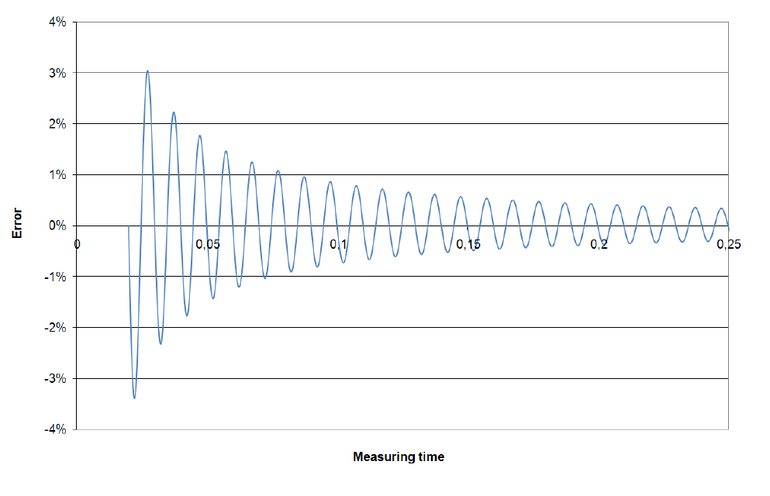
Figure 2 illustrates this: The (constant) rms value of a sinusoidal signal is measured, starting at a positive zero-crossing. The longer the measurement lasts, the smaller the deviation from the rms value becomes. For symmetry reasons, the error periodically shrinks to zero once one half-cycle of the signal has passed. Every 10 ms the 50 Hz signal in figure 2 is measured without error [1].
The graph also shows the worst-cases occurring by exceeding or undercutting the ideal value by about ¼ of a signal period. Provided synchronization is properly set, the magnitude of the resulting error is minor and already taken into consideration in the specified measuring accuracy.
Significance of the sampling rate in power analysis
Before judging whether or not a given sampling rate is sufficient to accurately measure all pulses of a VFD’s signal, we need to take a closer look at the measurement method and underlying mathematics. ZES ZIMMER’s application note #105 “Power measurement and its theoretical background“[1] provides a convenient introduction to the subject. In brief, rms values, DC values, active power and other values can be considered statistical quantities when discussing digital signal processing. They can be interpreted as average values of a (potentially conditioned, if necessary) signal. This is the “secret” of power analyzers: there is no need to get every single measurement right, as long as the average over a large enough set of samples is calculated properly. Let us take the example of the DC value of a signal to illustrate: Mathematically, the DC value is the average of an integral over a certain time period. In digital signal processing, the integral is a sum of random sample values of the signal. The same formula is used in statistics.
Let us carry out a number of thought experiments: imagine a very short pulse of 100ns duration with a repetition frequency of 16 kHz (i.e. one pulse every 62.5 µs). Digitizing this signal with an A/D converter at 3 MS/s over 0.5 s yields 1,500,000 samples. Assuming random sampling – no synchronization with the signal at all – we will see about 1,500,000/625 = 2.400 samples “hitting” the pulse. The expected error within a 99% confidence interval is only 6 samples. The additional error introduced is only 0.25%, allowing us to calculate all desired values (rms, active power …) without problems and with reasonable accuracy – as long as analog bandwidth is sufficient and sampling is truly random.
From time to time this causes some confusion regarding the sampling theorem (Nyquist-Shannon sampling theorem or WKS sampling theorem). The sampling theorem demands that a signal must be sampled with a rate at least twice as high as the signal bandwidth. The part often overlooked reads: “…in order to completely reconstruct the signal.” Therefore, the sampling theorem does not apply in our context, since reconstructing the original signal is not necessary in order to calculate the desired quantities. When calculating averages, the order of the addends is irrelevant (commutativity of addition) for the result.
However, in case further digital processing like FFT or filtering is intended, the criteria of the sampling theorem have to be met, and the use of an anti-aliasing filter is highly advisable in order to ensure they are.
The basic principle of random sampling is to record more values than seem necessary at first glance. This can lead to astonishing results. Already in the early years of digital measurement, highly accurate DC meters were designed on the base of 8-bit-A/D-converters. The signal then was overlaid with random noise or a saw-tooth wave with an amplitude equal to that of the least significant bit (LSB). Instead of measuring only once, which should be sufficient at first sight, the resulting signal was sampled several thousand times.
The outcome: A change in DC amplitude by e.g. 1/100 of the LSB amplitude resulted in one additional bit to be set per 100 sample values in average. This difference was counted and displayed. However, some criteria had to be observed: The analog hardware had to be sufficiently precise, the noise had to be random enough, and the number of samples – the statistical basis – significantly large.
What had been inevitable in the days of 8-bit A/D-converters due to the lack of higher resolution has still some relevance today for random sampling in the time domain. The analog hardware needs to be precise and must offer sufficient bandwidth. The samples ought to be random – i.e. statically independent from the signal, and the measurement interval must be long enough.
Although we learned that statistics permit to measure short pulses even with a low sampling rate, as long as measuring time is sufficiently long, the laws of physics cannot be ignored: An A/D converter operating at 10 kS/s will hardly have the required analog bandwidth to sample a pulse with a duration of 1 µs, nor will its sample & hold circuitry be fast and accurate enough. It is therefore always beneficial to use converters with a high sampling rate. Sampling will be faster and thus produce more results in a given time frame.
Another aspect is related to the measurement time: as mentioned above, measured values have a strongly statistical character, and as with all statistics, number of samples is pivotal for the quality of the results. The higher sampling rate and - time, the higher the number of samples taken during a measuring interval. Hence, a higher sampling rate may yield useful and accurate results within a relatively shorter period of time, or measure the DUT more accurately.
To conclude: when measuring high-frequency PWM signals, it cannot be guaranteed each and every pulse will be captured correctly – but for power measurements this is also not necessary. The power analyzer will calculate the statistical average over the cycle time (which cannot be chosen arbitrarily small) with great accuracy due to the high number of samples used for calculation.
[1] For the sake of completeness it should be mentioned that under certain well defined restrictions (symmetric 3-phase, without even harmonics) the measurement time can be shrunk to 1/6 of the signal period [2] and yet produce correct results.
References:
[1] Thomas Jäckle; Leistungsmessung und deren theoretischer Hintergrund (#105)
http://www.zes.com/download/applikationsberichte/zes_applicat_105_leistungsmessung_d.pdf
[2] João Afonso, Carlos Couto, Júlio Martins; “p-q Theory Power Components Calculations”;
ISIE’2003 - IEEE International Symposium on Industrial Electronics;
http://repositorium.sdum.uminho.pt/bitstream/1822/1864/1/ISIE-03_JLA.pdf
This article is also published in German language at www.elektronikpraxis.vogel.de