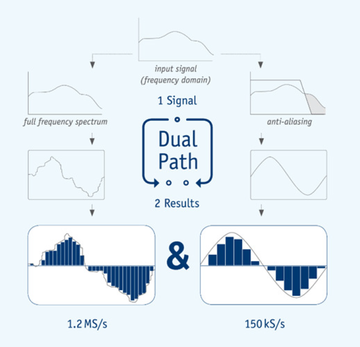
DualPath explained
Why one A/D converter per channel is not (always) sufficient
In conventional power analyzers, a signal first undergoes analog conditioning. Then the output is optionally fed through an antialiasing filter (AAF) before it gets digitized by an A/D converter and awaits further processing. The decision for or against the AAF has to be taken before sampling, as this is when aliasing occurs. It cannot be undone later on. RMS values can be determined without risk of aliasing due to their statistical nature, all other measurements need to be handled with care. Due to the limitation to a single A/D converter, there are inherently some downsides to be factored in with conventional devices. If the goal is to measure RMS power both over the entire bandwidth and at the fundamental frequency, unfiltered and filtered measurements could be alternated – in theory. In practice, it is of utmost difficulty to exactly reproduce the same operating point twice. Unless this can be guaranteed, all comparisons between results are void due to lack of repeatability. Besides, this procedure is extremely time-consuming. If one variant is skipped in order to save time, the results are inevitably error-prone. If the filter remains activated to avoid aliasing with the FFT, bandwidth gets sacrificed when measuring RMS values. Switching off the AAF voids the FFT. If it is carried out nevertheless, the quality of the results is questionable. An aliasing error of 50%, for instance, is easily detected, however a deviation of 0.5% could go unnoticed.
In the end, all of the aforementioned measurement methods are merely unsatisfactory compromises. This is why ZES ZIMMER has fundamentally redesigned signal processing and developed the DualPath architecture. The analog side is the same as in conventional measuring devices, however the subsequent digital processing has been revolutionized. Only power analyzers of the LMG600 series are equipped with two A/D converters in two independent signal paths for each current and voltage channel. One, for the filterless measurement of the wideband signal, and another, for the narrowband signal at the output of the antialiasing filter. The parallel processing of the digitized sample values gives the user access to both measurements of the same signal, without risking aliasing effects.
This unique procedure avoids all of the downsides of previous approaches and guarantees the most precise result in the shortest time possible.
Frequently asked questions
- Manufacturer X claims his instruments have been capable of displaying RMS power and harmonics in parallel for years – isn’t this basically the same as DualPath? No, it merely means the customer does not have to switch between measurement modes to see all desired values at the same time. This parallel view is convenient for the user, but a closer look reveals that the shown RMS values omit important portions of the power spectrum. The culprit is the AAF, whose activation is required to ensure the validity of the harmonics analysis. This filter limits bandwidth to several hundred kilohertz, which also affects the displayed RMS values. Those are not, like in case of the LMG600, true broadband values comprising the entire power spectrum between DC and 10 MHz. Especially when looking at PWM signals with a switching frequency of up to 20 kHz, like those occurring at the output of frequency converters, the portion from 300 kHz to 10 MHz should not be neglected.
The instruments of manufacturer Y are sampling with all filters removed, and allow you to apply digital filtering later on in order to isolate narrowband values – does this not achieve the same results as DualPath? No, it merely proves the Nyquist-Shannon theorem and the subject of aliasing have not been properly grasped. Frequency portions for whom the sampling rate is insufficient according to the theorem need to be removed prior to filtering, as they can no longer be identified after sampling. E.g. a signal at 50 Hz below the sampling rate would show up at 50 Hz after sampling. This signal, which has been created by undersampling, is indistinguishable from the original signal, since part of the original information has been wiped out due to the insufficient sampling rate.
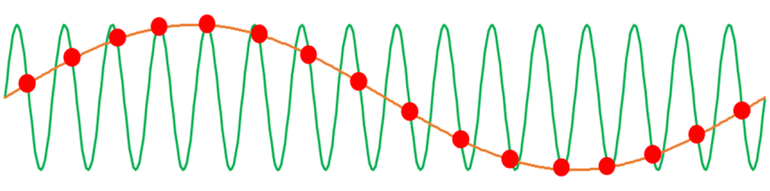
The following picture illustrates this effect:
The green line represents a high-frequency (2 MHz) signal before sampling, the red dots show the result of undersampling – here with a rate slightly higher than the signal frequency (2.125 MHz). The erroneous sampling process, since too slow according to the Nyquist-Shannon theorem, creates a “phantom signal” at a frequency of (2.125 MHz – 2 MHz = 125 kHz), which is merely 1/16 of the original frequency and can no longer be distinguished from the genuine signal content around 125 kHz. In that range, e.g. harmonics of a frequency converter’s switching frequency might appear, which would in turn be distorted by the “phantom signal”. The knowledge that part of the power measured around 125 kHz stems from the undersampled 2 MHz signal is irretrievably lost. The above values are merely examples, the erroneous frequency components might as well appear near the fundamental of the unit under test. Trying to identify these components after the fact and to remove them would be as futile as striving to identify blue objects on a color photography reduced to black and white – the information “color“ is irretrievably lost, the
remaining information “brightness“ is by no means equivalent.