Frequenzumrichter
Elektrische Leistung und Wirkungsgrad am Frequenzumrichter zuverlässig messen
Verfasser: Dipl.-Ing. Thomas Jäckle, Leiter Forschung und Entwicklung
Durch den vermehrten Fokus von Politik und Öffentlichkeit auf ungenutzte Einsparpotenziale elektrischer Verbraucher ist unter anderem die Verwendung von Frequenzumrichtern zur verlustarmen, drehzahlvariablen Regelung von Elektromotoren in den Vordergrund gerückt. Die Hersteller von Motoren und Antriebssystemen sind gefordert, den Wirkungsgrad ihrer Produkte zu optimieren, und benötigen hierfür im Gegenzug geeignete Messmittel zur Bewertung von Leistung und Verlusten. Der Einsatz von Umrichtern kann die Effizienz des Gesamtsystems verbessern, erhöht jedoch gleichzeitig die Komplexität und stellt höhere Anforderungen an die einzusetzenden Messverfahren und –mittel.
Hinsichtlich der geeigneten Vorgehensweise und der Bewertung der Ergebnisse stellt sich eine Reihe von Fragen:
Wie lässt sich die Messunsicherheit zuverlässig abschätzen? Können auch PWM-Pulse kurzer Dauer korrekt richtig erfasst werden? Wie wirken sich Einstellungen des Messgerätes auf das Ergebnis aus? Ist die verwendete Abtastrate überhaupt ausreichend?
Der folgende Applikationsbericht beantwortet nicht nur diese aufgeworfenen Fragen sondern vermittelt darüber hinaus auch das nötige Hintergrundwissen für ein breiteres Verständnis der elektrischen Leistungsmessung im Allgemeinen.
Betrachtungen der Messunsicherheit in Abhängigkeit von der spektralen Energieverteilung
Sollen Verbesserung des Wirkungsgrades im Bereich von Prozentbruchteilen erzielt werden, so ist es unerlässlich, zunächst die Genauigkeit der verwendeten Messverfahren gründlich unter die Lupe zu nehmen. Alle Betrachtungen zur Ermittlung der Leistung sind auch für die Berechnungen von Wirkungsgraden relevant, da es sich bei ihnen letztlich um Quotienten aus Ausgangs- und Eingangsleistungen handelt. Die Messunsicherheiten der Leistungsmessgeräte werden von den Herstellern nur für sinusförmige Größen angegeben, da die nationalen Normale, auf die ihre Genauigkeit letztlich zurückgeführt wird, in der Regel auch nur sinusförmige Größen darstellen können. Trotz dieser Einschränkung kann man aber einige Überlegungen anstellen, um die Unsicherheit sinnvoll abschätzen zu können.
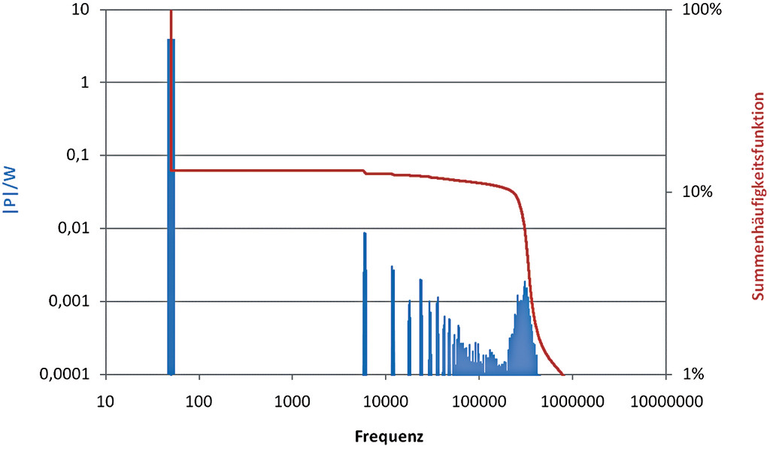
Die spektrale Verteilung der Leistung am Ausgang des Frequenzumrichters (FU) zeigt folgenden Verlauf. Die genauen Zahlen hängen natürlich von der konkreten Applikation ab, das Prinzip ist aber immer das gleiche.
Den wichtigsten Beitrag zur Wirkleistung liefert die Grundschwingung des Motors. Geht man von einem Umrichter aus, der den Motor mit gutem Wirkungsgrad ansteuert, so wird ein Großteil der Energie vom FU zum Motor bei dieser Frequenz transportiert. Diese Frequenz liegt in der Regel im Bereich unter 1000 Hz und weist gewöhnlich geringe Oberschwingungsanteile auf.
Die nächste Position ist die Taktung des Umrichters selbst. Diese liegt zwischen wenigen hundert Hertz (bei FU mehrerer MW Leistung) und 20 kHz (bei Leistungen im kW-Bereich) und ist durch die annähernd rechteckförmigen Signale der Pulsweitenmodulation stark mit Oberschwingungen belastet.
Und schließlich gibt es Signalanteile, die durchaus bis in den MHz-Bereich reichen und verschiedene Ursachen haben können: Resonanzen in den Motorwicklungen durch die rechteckförmigen Signale, Flankensteilheiten, Reflexionen am Ende der Leitungen, uvm.
Prinzipiell können nur gleichfrequente Strom- und Spannungsanteile eine Wirkleistung ausbilden. Unterhalb von 1000 Hz sind diese Ströme natürlich vorhanden, der Motor soll sich ja drehen. Im Bereich der Taktfrequenz hängt die Stärke der Ströme stark von der Induktivität, der Wicklungskapazität sowie der Erdkapazität der Motorwicklung ab. Die Ströme sind also zum einen gedämpft, zum anderen auch noch induktiv oder kapazitiv phasenverschoben. Wichtig ist, dass sie bei Weitem nicht so viel Leistung beisteuern wie die Grundschwingung. Über den noch höheren Frequenzbereich kann man allgemein feststellen, dass die Stromamplitude in der Regel klein sein wird, was zusammen mit den üblicherweise relativ niedrigen Spannungen – wenn überhaupt – nur eine sehr geringe Wirkleistung bewirken kann.
Für Abbildung 1 wurde ein relativ kleiner Motor an 50 Hz im Leerlauf (4 W) betrieben. Der FU wird mit ca. 6 kHz getaktet und treibt den Motor über 100 m Leitung an. Durch diese in der Praxis eher unüblichen Werte wurden mehrere Dinge erreicht: Die Signalkomponenten der Taktfrequenz (6 kHz, 12 kHz, 18 kHz, ...) stechen im Spektrum (im Diagramm blau eingefärbt) stärker gegenüber der Grundschwingung hervor als bei einem Motor unter Last. Trotzdem nimmt die Amplitude von 6 kHz bis 150 kHz stetig ab. Der nachfolgende Anstieg mit einem Maximum bei 340 kHz wird durch Reflexionen auf der exemplarisch bewusst lang gewählten Leitung verursacht.
Die rote Kurve zeigt die (invertierte) Summenhäufigkeitsfunktion der Leistung: Der größte Teil der Leistung (87%) entfällt auf die Grundfrequenz von 50 Hz, die übrigen 13% liegen oberhalb dieser Frequenz. Mit Beginn der Taktfrequenz bei 6 kHz nimmt die verbleibende Leistung stetig ab. In diesem Beispiel gibt es noch einmal einen sehr großen Leistungsanteil um 310 kHz, dort sinkt die verbleibende Leistung von ca. 11% auf ca. 1%.
Die maximale Amplitude dieser Leistung bei 310 kHz ist zwar geringer als bei 6 kHz, jedoch ist die Bandbreite wesentlich größer, so dass in Summe hier deutlich mehr Leistung umgesetzt wird als bei der Taktfrequenz.
Die hier vorgestellten Werte sind, wie bereits erwähnt, eher untypisch für reale Motoren. So hängt die Leistung durch Reflexionen natürlich sehr stark von der Leitungslänge ab, und Leitungslängen von 100 m sollte eher die Ausnahme als die Regel sein. Wichtig ist das Grundprinzip: Zur Beurteilung der Unsicherheit muss zunächst einmal gemessen werden, welche Frequenzanteile vorhanden sind.
Nach der spektralen Zerlegung der FU-Signale lässt sich für jeden Frequenzbereich abschätzen, wie groß sein Beitrag zur Unsicherheit ist. Bei der sinusförmigen Grundschwingung als wichtigstem Signalanteil gelingt das sehr gut, bei höherfrequenten Signalen gelingt es nur näherungsweise, wobei dort leichte Fehler in der Abschätzung vernachlässigbar sind, wie die nachfolgenden Beispiele zeigen.
Beispiel 1
Es sei folgende Verteilung über die Frequenz ermittelt worden:
₋ 4 W bei einer 5Hz-Grundschwingung
₋ 0,1 W bei der Taktfrequenz und ihren Harmonischen im Bereich von 6 kHz bis 150 kHz
₋ 0,03 W durch hochfrequente Effekte bei 350 kHz
Der für den anzuwendenden Leistungsmessbereich anzusetzende Wert sei mit 8 W angenommen. Informationen über Messunsicherheit bei nicht-sinusförmigen Signalen sind in jedem Benutzerhandbuch der ZES ZIMMER Leistungsmessgeräte zu finden. Die Messunsicherheitsdaten in der untenstehenden Tabelle wurden dem LMG500 Benutzerhandbuch entnommen.
| Frequenzbereich |
0,05 Hz...45 Hz, 65 Hz...3 kHz |
45 Hz...65 Hz | 15 kHz...100 kHz | 100 kHz...500 kHz |
|
Fehler der Wirkleistung ±(% vom Messwert + % vom Messbereichsendwert) |
0,028+0,03 | 0,015+0,01 | 0,24+0,3 | 0,8+1,0 |
Für die Grundschwingung ergibt sich eine Unsicherheit von 0,028% von 4 W = 1,12 mW. Für die Taktfrequenz und ihre Harmonischen wird der Einfachheit halber die Unsicherheit für den Frequenzbereich ab 15 kHz gewählt, obwohl die Grundschwingung bei 6 kHz liegt. Der dadurch etwas zu groß abgeschätzte Fehler wird durch die Frequenzanteile über 100 kHz kompensiert, die etwas zu klein angenommen werden. Das erspart eine weitere Zerlegung und vereinfacht die Rechnung für dieses Beispiel etwas. Für die Taktfrequenz beträgt die Unsicherheit somit 0,24% von 0,1 W = 0,24 mW, und für die hochfrequenten Effekte ergibt sich eine Unsicherheit von 0,8% von 0,03 W = 0,24 mW.
Zu diesen Messunsicherheiten der einzelnen Signalanteile muss für eine seriöse Abschätzung auch noch die Messunsicherheit aus dem Messbereich selbst addiert werden. Dies geschieht anhand der Werte der Signale mit den größten Amplituden, hier also bei 5 Hz: 0,03% von 8 W = 2,4 mW. Es ergibt sich also eine Gesamtmessunsicherheit von 4 mW. Die einzelnen Beiträge hierzu sind:
| Grundfehler: | 2,40 mW/4 mW = | 60% |
| Fehler der Grundschwingung: | 1,12 mW/4 mW = | 28% |
| Fehler der Taktfrequenz: | 0,24 mW/4 mW = | 6% |
| Fehler der hochfrequenten Effekte: | 0,24 mW/4 mW = | 6% |
Dieses Beispiel wäre für einen Grundschwingungsfrequenzbereich von 0,05 Hz...3 kHz gültig. Für Frequenzen von 45 Hz...65 Hz gelten die Werte des nachfolgenden Beispiels.
Beispiel 2
Wie Beispiel 1, jedoch 50 Hz Grundschwingung.
Für die Grundschwingung ergibt sich eine Unsicherheit von 0,015% von 4 W = 0,6 mW. Der Fehler aus dem Messbereich sinkt auf 0,01% von 8 W = 0,8 mW, und die Gesamtmessunsicherheit beträgt 1,88 mW. Die einzelnen Beiträge hierzu sind:
| Grundfehler: | 0,80 mW/1,88 mW = | 42% |
| Fehler der Grundschwingung: | 0,60 mW/1,88 mW = | 32% |
| Fehler der Taktfrequenz: | 0,24 mW/1,88 mW = | 13% |
| Fehler der hochfrequenten Effekte: | 0,24 mW/1,88 mW = | 13% |
Durch die Halbierung des Gesamtfehlers treten die hochfrequenten Anteile natürlich stärker zu Tage, jedoch bleibt der überwiegende Fehleranteil bei 50 Hz dominierend. Ob der Fehler aus dem Takt jetzt 0,24 mW ist oder einfach mit 0,3 mW abgeschätzt wird, bedeutet beim Takt zwar 25% Unterschied, beim Gesamtfehler aber nur noch 3%!
Bleibt noch die Frage, wie man die genaue Verteilung der Signale im Spektrum ermittelt, zumal es sich ja nicht bei allen um Harmonische handelt. Eine Möglichkeit wäre der Einsatz von Filtern: Man misst zunächst mit einem relativ schmalbandigen Filter (Grenzfrequenz knapp unter der Taktfrequenz, z.B. 1 kHz) die reine Grundschwingung und deren Harmonische aus. Dann kann man mit einem breitbandigeren Filter den Takt hinzunehmen (z.B. 150 kHz Grenzfrequenz) und aus der Differenz der Leistungswerte den Leistungsanteil der Taktfrequenz berechnen.
Die Verteilung in Abbildung 1 wurde auf anderem Wege erzeugt: Mit einem Präzisions- Leistungsmessgerät LMG500 und der Software LMG-CONTROL (mit Option Waveform-Analysis) wurde das Spektrum der Leistung von 50 Hz bis 1,5 MHz in 50Hz-Schritten ermittelt. Dadurch erhält man ein in 30.000 Linien aufgelöstes, sehr detailliertes Spektrum.
Die prinzipielle Berechnung der Gesamtmessunsicherheit bei nicht sinusförmigen Mischsignalen ist in den jeweiligen Gerätehandbüchern genau beschrieben und in obigen Beispielen auf ein LMG500 angewendet worden.
Bedeutung von Messdauer und Zykluszeiten
Bei der Wahl der Messdauer können prinzipiell zwei Dinge passieren, die verhindern, dass man über eine ganzzahlige Anzahl von Signalperioden misst: Zum einen kann die Synchronisation falsch eingestellt sein, so dass gar nicht oder auf eine falsche Frequenz synchronisiert wird. Zum anderen könnte die Signalperiode länger als die Zyklusdauer werden, so dass nur ein Bruchteil einer Periode erfasst wird ‑ ein Signal mit beispielsweise 0,55 Hz kann man innerhalb einer Sekunde nicht korrekt messen! Diesen Fall kann man einfach durch eine angepasste Zykluszeit vermeiden.
Sollte eine Synchronisation gar nicht oder nur schlecht möglich sein, kann durch eine entsprechend längere Zykluszeit der Fehler verringert werden. Angenommen, dass um 0,1 Perioden falsch gemessen wird, so ist der Fehler bei einer Messung über 1,1 Perioden natürlich größer als bei einer Messung über 100,1 Perioden!
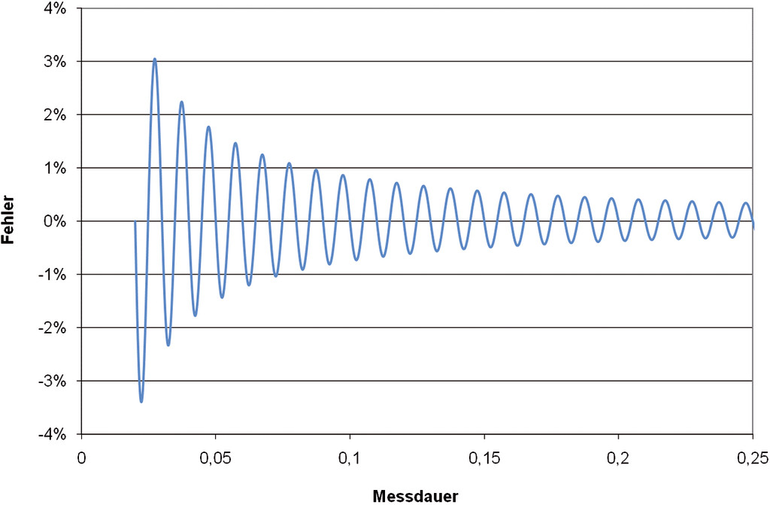
Abbildung 2 verdeutlicht diesen Effekt: Der Effektivwert eines Sinussignals wird, beginnend mit einem positiven Nulldurchgang, vermessen. Je nachdem, wie lange man misst, treten mit längerer Messzeit immer kleinere Fehler gegenüber dem konstanten Effektivwert des Signals auf. Wenn jeweils exakt über eine ganze (oder halbe) Periode [1] gemessen wird, so ist dieser Fehler natürlich Null. Im Beispiel wird ein 50Hz-Signal verwendet, bei dem alle 10 ms exakt richtig gemessen wird.
In diesem Graphen sind auch die Worst-Case-Messzeiten enthalten, wenn man z.B. eine Viertelperiode zu lang oder zu kurz misst. Bei einer richtig eingestellten Synchronisation ist dieser Fehler um Größenordnungen kleiner und bereits in den spezifizierten Messunsicherheiten enthalten.
Stellenwert der Abtastrate bei der Leistungsmessung
Zur Beantwortung der Frage, ob man mit einer gegebenen Abtastrate überhaupt alle Pulse eines PWM-Signals hinreichend genau vermessen kann, ist es zunächst einmal wichtig, das Messverfahren und die zugrundeliegende Mathematik zu betrachten. Zu den Grundlagen wird hier insbesondere auf den ZES ZIMMER Applikationsbericht #105 [1] verwiesen, der diese Hintergründe ausführlich beleuchtet. Kurz zusammengefasst kann man sagen, dass Effektivwerte, DC-Werte, Wirkleistung und andere Werte im Rahmen der digitalen Signalverarbeitung nur noch statistische Größen sind. Sie werden jeweils als Mittelwert eines gegebenenfalls aufbereiteten Signals ausgedrückt. Und genau hier liegt das „Geheimnis“ aller Messgeräte: Es ist überhaupt nicht notwendig, zu jedem Zeitpunkt das Signal exakt zu messen, man muss es nur im Mittel richtig erfasst haben! Sehr anschaulich kann man das am Beispiel des DC-Wertes zeigen: Ist der DC-Wert exakt ausgedrückt noch der Mittelwert des Integrals über einen Zeitraum, wird bei einer digitalen Signalverarbeitung aus dem Integral eine Summe über die Abtastwerte, die Stichproben aus dem Signal darstellen. Und diese Summengleichung stimmt exakt mit den Gleichungen überein, die in der Statistik benutzt werden.
Dazu ein paar Gedankenexperimente: Man hat einen sehr kurzen Impuls von nur 100 ns Dauer, der mit 16 kHz (also alle 62,5 µs) wiederholt wird. Nimmt man dieses Signal mit einem AD-Wandler mit 3 MS/s auf und misst über 0,5 s, so bekommt man 1.500.000 Abtastwerte. Tastet man zufällig ab (also nicht z.B. per PLL auf das Signal synchronisiert), so werden statistisch 1/625 der Abtastwerte die Amplitude des Pulses zeigen, das sind also 2400 Werte. Der dabei zu erwartende Fehler innerhalb eines Konfidenzintervalles von 99% beträgt hierbei nur 6 Samples. Das ist ein zusätzlicher Fehler von nur 0,25%. Mit dieser Datenbasis lassen sich alle statistischen Werte (Effektivwert, Wirkleistung, ...) ohne Probleme und mit sehr guter Genauigkeit berechnen. Voraussetzung ist natürlich, dass die analoge Bandbreite der Messkanäle hinreichend groß ist und man zufällig abtastet (Random Sampling).
In diesem Zusammenhang kommt es immer wieder zu Missverständnissen durch eine falsche Anwendung des Abtasttheorems (auch Nyquist-Shannon-Theorem oder WKS-Abtasttheorem). Dieses besagt, dass man ein Signal mit einer Rate abtasten muss, die mindestens der doppelten Signalbandbreite entspricht. Was hier leider oft weggelassen wird, ist der entscheidende Nachsatz „…, um es wieder rekonstruieren zu können.“ Daher kommt das Abtasttheorem hier nicht zur Anwendung: zur Ermittlung statistischer Größen muss man das Signal nicht vollständig rekonstruieren, da es für die Berechnung eines Mittelwerts irrelevant ist, in welcher Reihenfolge die einzelnen Werte aufsummiert werden (Stichwort Kommutativgesetz).
Etwas anderes ist es natürlich, wenn man das Signal digital im Sinne einer FFT oder Filterung verarbeiten möchte. In diesem Fall sind die Forderungen des Abtasttheorems sehr wohl einzuhalten, und man ist sehr gut beraten, dies durch die Verwendung eines Anti-Aliasing-Filters zu garantieren.
Die Grundidee des Random Sampling ist, dass man viel mehr Werte aufnimmt, als eigentlich nötig erscheinen. Dieses Verfahren kann erstaunliche Dinge bewirken. So wurden beispielsweise schon in den Anfängen der digitalen Messtechnik hochgenaue DC-Messgeräte gebaut, die jedoch nur einen 8-Bit-A/D-Wandler besaßen. Hier wurde auf das DC-Signal bewusst noch ein Sägezahn oder ein Rauschen addiert, welches im Bereich der Amplitude des niederwertigsten Bit (LSB - least significant bit) lag. Anstatt das Signal mit nur einer A/D-Wandlung zu messen, was ja zunächst hinreichend erscheint, wurde das verrauschte Signal viele tausend Mal abgetastet.
Der Effekt war nun folgender: Stieg die DC-Amplitude z.B. um 1/100 der Amplitude des LSB an, so wurden im Mittel 1/100 der einzelnen Samplewerte ebenfalls mit einem Bit mehr als vorher abgetastet. In der Statistik über die Abtastwerte konnte man diesen Anstieg direkt ablesen. Auch hier gelten natürlich einige Randbedingungen: Die Analoghardware musste genau genug, das Rauschen zufällig – insbesondere statistisch unabhängig vom Messsignal - und die Anzahl der Abtastwerte als statistische Basis, groß genug sein.
Was zu Zeiten von 8-Bit-A/D-Wandlern im Amplitudenbereich mangels höher auflösender Wandler notwendig war, wird heute bei modernen Leistungsmessgeräten mit dem Random Sampling im Zeitbereich gemacht: Die Analoghardware muss genau und breitbandig genug, die Abtastwerte müssen gegenüber dem Signal zufällig genug und die Messzeit muss lang genug sein.
Obwohl es rein statistisch also möglich sein sollte, mit einer sehr geringen Abtastrate bei entsprechend langer Messzeit auch kurze Impulse korrekt zu erfassen, darf man hier die Physik nicht ganz außer Acht lassen: Ein Wandler mit 10 kS/s wird in der Praxis weder die analoge Bandbreite haben, um einen 1 µs Puls zu erfassen, noch wird die Sample&Hold-Schaltung eines solchen Wandlers schnell und genau genug arbeiten. Es wird sich also in der Praxis immer auszahlen, auf eine ausreichend hohe Abtastrate zu achten, da nur derartige Wandler überhaupt in der Lage sind, solch kurze Pulse physikalisch zu erfassen.
Ein weiterer Aspekt betrifft die Zykluszeit (Messdauer): Wie oben erwähnt haben die Messwerte stark statistischen Charakter. Und wie bei jeder Statistik ist die Datenbasis natürlich entscheidend für die Qualität der Ergebnisse. Die Anzahl der Abtastwerte während eines Messintervalls ist abhängig von der Dauer des Messintervalls sowie der Abtastrate. Mit einer hohen Abtastrate kann man folglich in kürzerer Zeit sinnvolle Ergebnisse erhalten und somit seinen Prüfling zeitlich feiner vermessen.
Um den Kreis zur einleitenden Frage zu schließen: Bei einem hochfrequenten PWM-Signal kann nicht sichergestellt werden, dass jeder einzelne Puls korrekt gemessen wird - dies ist aber für eine exakte Bewertung der Leistung auch nicht nötig. Über die nicht beliebig kurz wählbare Zykluszeit des Messgerätes wird das Signal im statistischen Mittel durch die hohe Anzahl der in die Berechnung eingehenden Abtastwerte trotzdem sehr genau erfasst.
[1] Der Vollständigkeit halber sei erwähnt, dass in einer exakt symmetrischen 3-Phasenschaltung und der Einschränkung, dass das Messsignal keine geradzahligen Harmonischen enthält, die Messzeit auf 1/6 der Signalperiode (aber auch nicht weniger!) verkürzt werden kann [2].
Literaturangaben
[1] Thomas Jäckle; Leistungsmessung und deren theoretischer Hintergrund (#105) http://www.zes.com/download/applikationsberichte/zes_applicat_105_leistungsmessung_d.pdf
[2] João Afonso, Carlos Couto, Júlio Martins; “p-q Theory Power Components Calculations”; ISIE’2003 - IEEE International Symposium on Industrial Electronics; http://repositorium.sdum.uminho.pt/bitstream/1822/1864/1/ISIE-03_JLA.pdf
Diesen Artikel in deutscher Sprache finden Sie auch bei www.elektronikpraxis.vogel.de